Level-Set-Evolutionen zur Lösung von Optimierungsaufgaben unter Nebenbedingungen
- Forschungsthema:Rekonstruktion teilspiegelnder Oberflächen
- Typ:Studienarbeit
- Betreuer:Dr. rer. nat. Jonathan Balzer
Dipl.-Ing. Stefan Werling
Thema der Arbeit
Viele Aufgaben der automatischen Sichtprüfung und Bildverarbeitung lassen sich mit Methoden der Variationsrechnung lösen. Meist wird auf einer regulären Kurve/Fläche S gerechnet. Gesucht ist ein S*, so dass
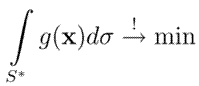
mit einer geeigneten Kostenfunktion g. Da i. A. keine Randaten vorliegen, konvergiert die abgeleitete Iteration meist gegen ein lokales Minimum. Das globale Optimum wird durch Regularisierung in Form einer Eindeutigkeit erzwingenden Nebenbedingung erhalten. Die theoretischen Grundlagen werden in [1] gelegt. Im Einzelnen umfasst die Arbeit folgende Teilaufgaben:
- Einarbeitung in den mathematischen Kontext (Optimierungsrechnung und Level-Set-Evolutionen),
- Implementierung eines Gradientenprojektionsverfahrens in Form einer Level-Set-Evolution und Erweiterung einer bestehenden MATLAB-Toolbox,
- Rechnen eines Beispiels aus dem Bereich der SichtprÄufung (z. B. Deflektometrie).
Die Arbeit richtet sich an Studierende der Elektrotechnik, Informatik oder Technomathematik. Die Bearbeitung soll in enger Kooperation mit dem Fraunhofer IITB durchgeführt werden. Über die Ergebnisse ist in einem Vortrag im Rahmen des Seminars am Lehrstuhl für Interaktive Echtzeitsysteme zu berichten.
Literatur
[1] J. E. Solem, N. C. Overgaard. A Gradient Descent Procedure for Variational Dynamic Surface Problems with Constraints In IEEE Proc. Workshop on Variational, Geometric and Level Set Methods in Computer Vision, pages 332-343,2005.
